Come and delve into understanding the big questions cosmologists try to answer: What is our Universe made of? Where does it come from and what is its future?
Our scientists have written these articles for you to grasp some of the answers they found. These articles are classified according to their level of difficulty so that everyone can find how much they want to get lost in the meanders of the Universe.
All levels
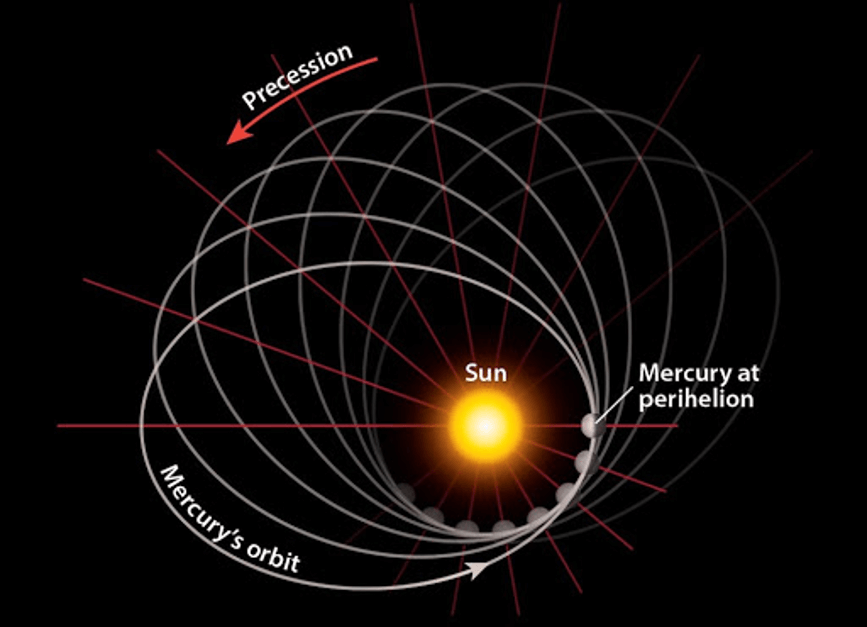
What if Einstein was wrong?
Yes, I have asked the question: what if the most widely recognized physicist ever was actually wrong? Perhaps wrong is too hard of a word,...

A quiet and sparkling sky
Recently, at the end of a yoga class, the teacher talked about balance between unchanging and transient states. It could not relate more to what...

Lurking in the dark
The hunt for new physics in the dark sector The standard model of particle physics, which describes the nature and interaction of sub-atomic particles, is...

Death to the standard model of the Universe (?): a murder mystery
Do not be frightened: choose wisely and you may only need to read half of this As a cosmology PhD student, I spend my days...

From Icelandic mines to the hidden depths of the Universe
Did you ever own a mineral collection? My cousin used to have one when he was a kid. His favourite was the Iceland spar, a...
Intermediate (is aware of physics concepts)
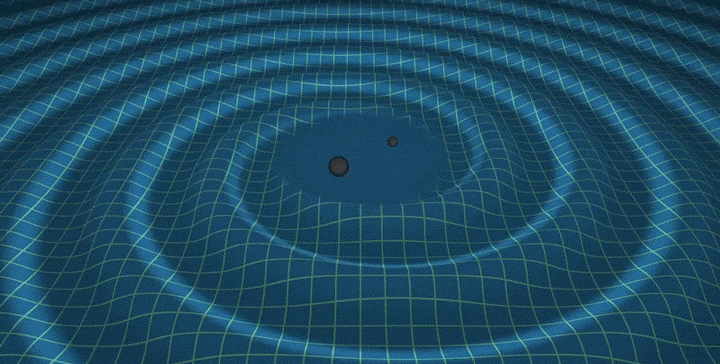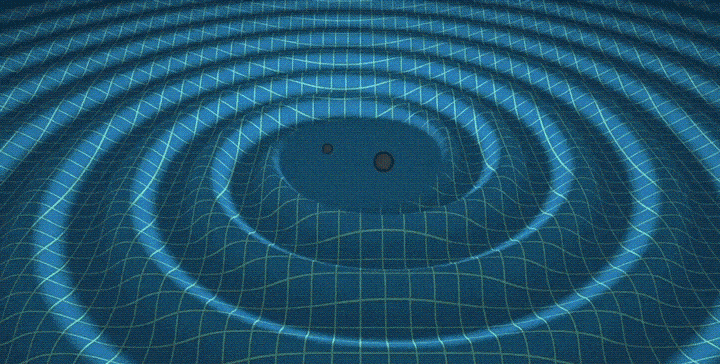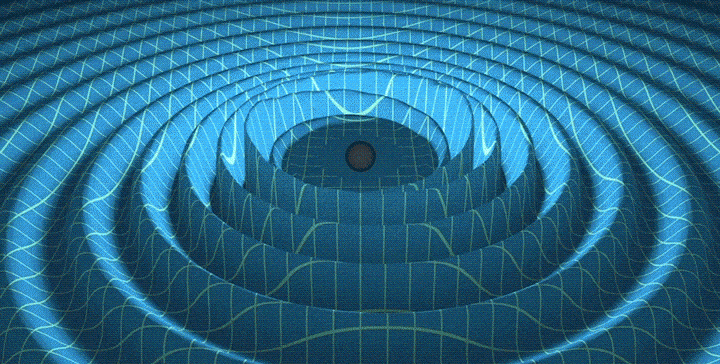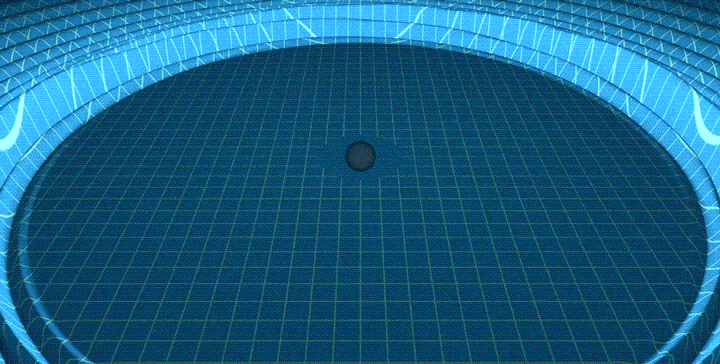
Galactic radio FM: tuning in to black holes
We have converted our galaxy into an enormous antenna. Then, we have used that antenna to detect the gravitational wave background generated by the merger...

Gamma-ray bursts – Nature’s most powerful fireworks
A flash in the sky. With such high energy that our eyes cannot detect it, as it is outside of their electromagnetic range. But gamma-ray...

Black Holes, Windows to New Observational and Theoretical Frontiers
Physics is the science of understanding Nature through mathematical formulations. Here understanding amounts to make a model within a given theoretical framework, analyzing the model...
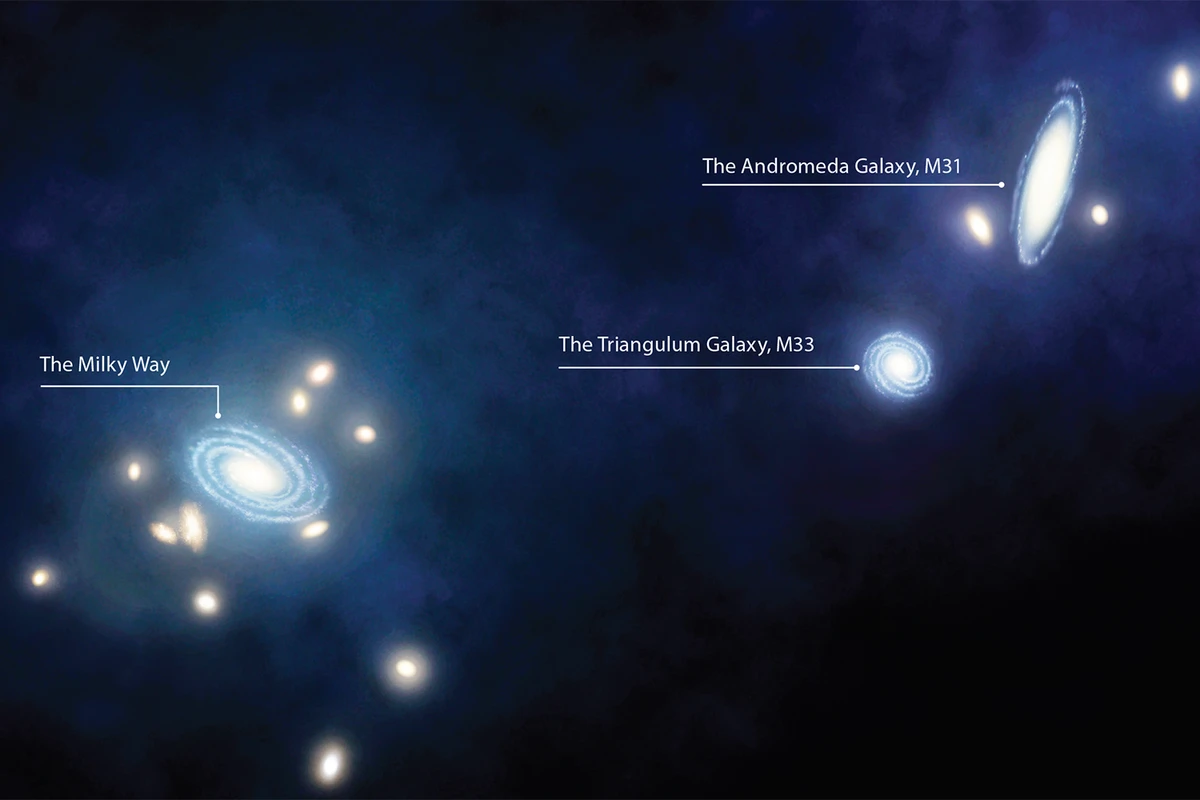
How our galaxy and its neighbours help us understand dark energy
Have you ever wondered about the forces that shape our universe and drive its expansion? I am here to share with you some fascinating insights...
Advanced (knows cosmology terminologies)
Did the Big Bang and cosmic inflation really happen?
(A tale of alternative cosmological models) . “The evolution of the world can be compared to a display of fireworks that has just ended: some...
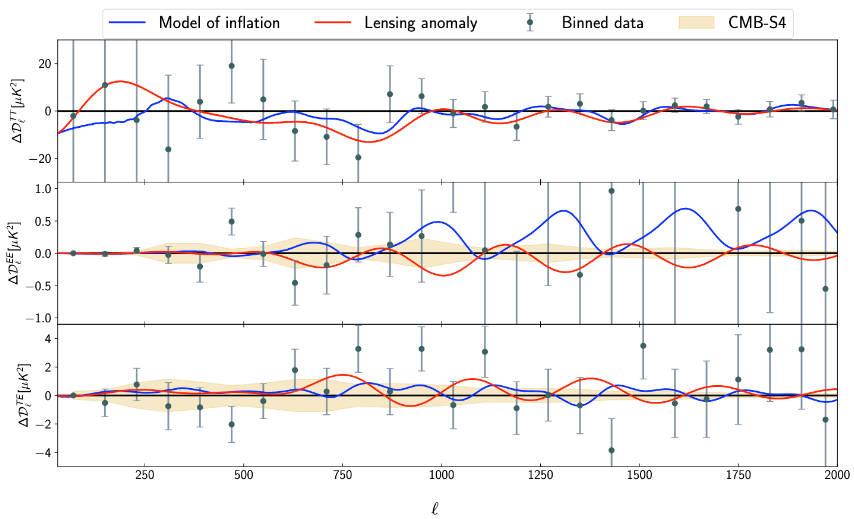
One Spectrum to cure them all: a primordial solution to cosmological anomalies and tensions
Our present understanding of the Universe is shaped by cosmological observations. Based on a model (built with well established theories + certain supporting assumptions) we...

Quantum vacuum: the cosmological constant problem
(A desperate attempt at explaining infinity in finite terms…) 1 Einstein and the cosmological constant I invite the nonexpert reader to a short but intense...
Is modified gravity an illusion?
Cosmology has been developed for thousands of years and there have been dozens of theories proposedto describe the observable universe. Starting from the Babylonian cosmology...
There are no "coincidences" in the universe
These are interesting times for cosmologists. On the one hand, general relativity and the cosmological principle of homogeneity and isotropy on sufficiently large scales has...
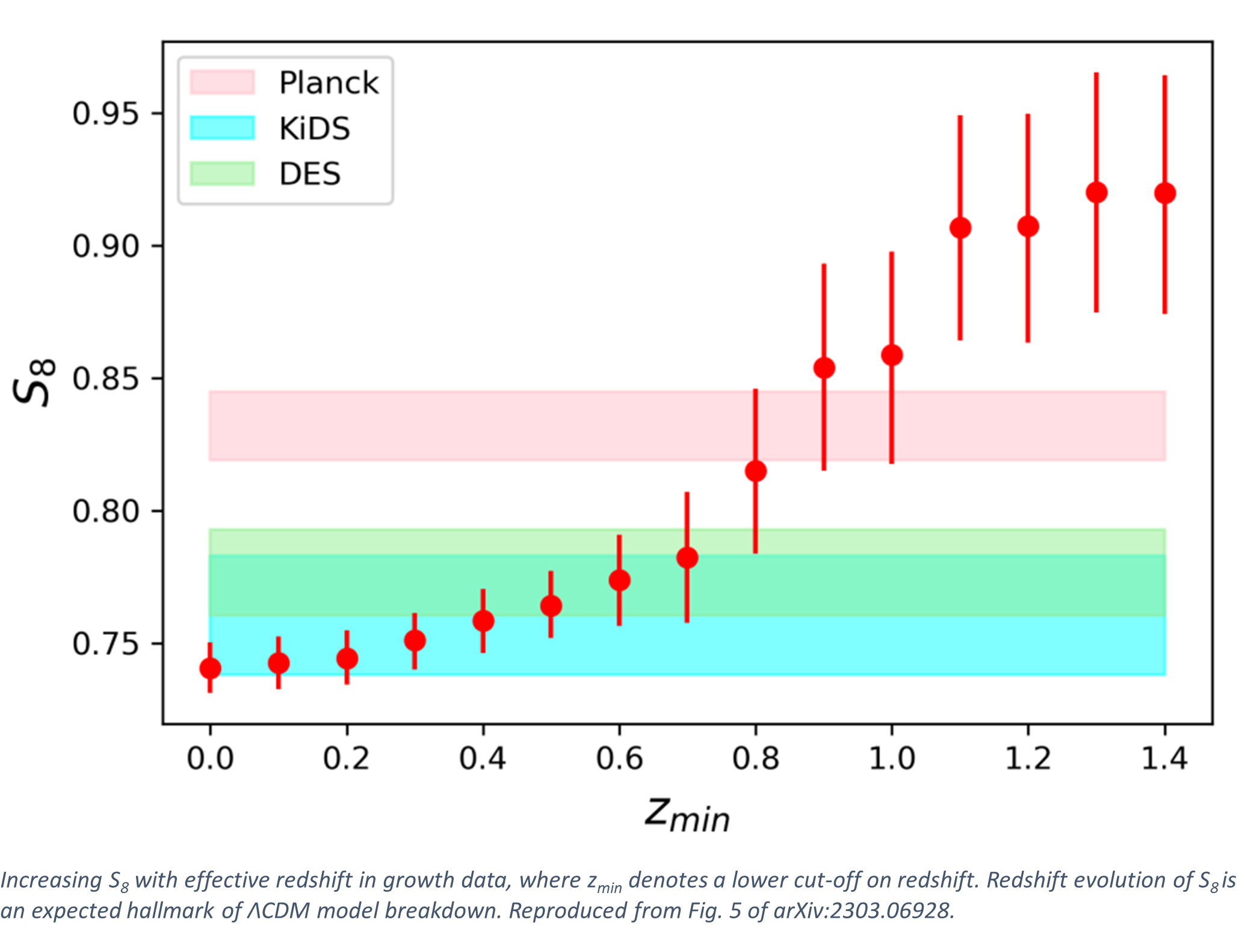
Reading the tea leaves in ΛCDM tensions
The field of cosmology appears to be in flux. The standard model ΛCDM, which is based on the cosmological constant Λ and cold dark matter...
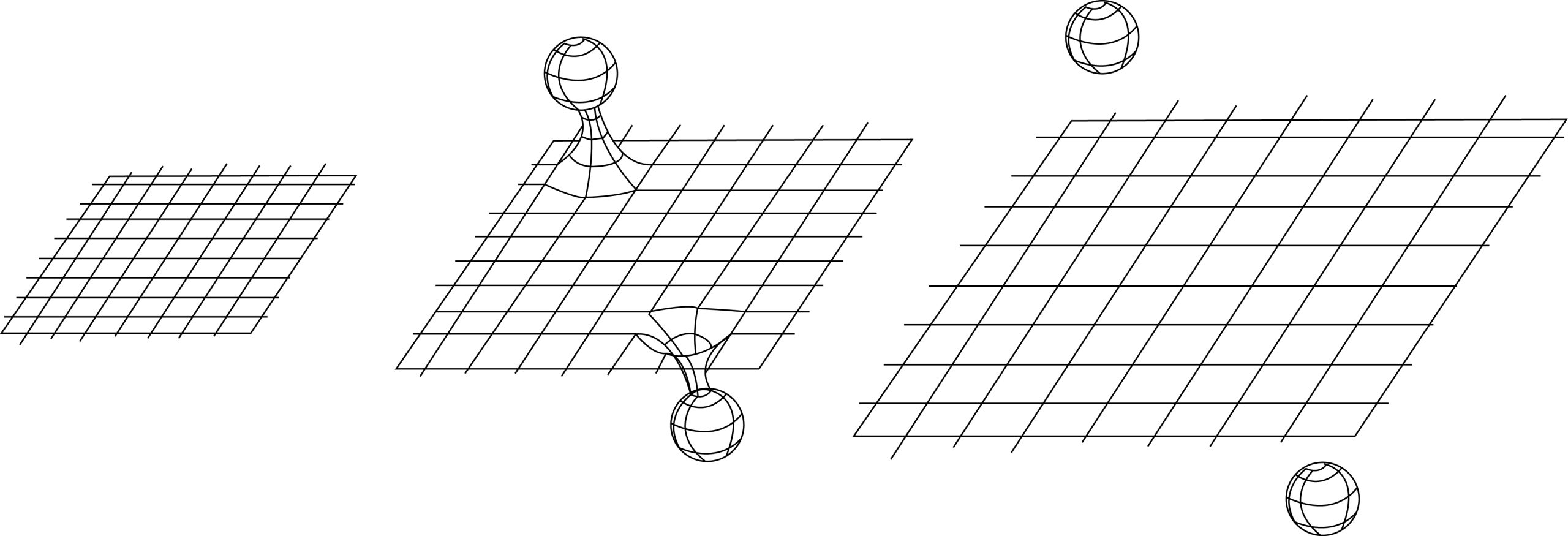
Quantum effects in the Universe
Einstein’s theory of General Relativity (GR) has not only changed our view on gravity but also had deep impact on the construction of modern physical...
