We have converted our galaxy into an enormous antenna. Then, we have used that antenna to detect the gravitational wave background generated by the merger of thousands of pairs of supermassive black holes, each situated at the centre of a galaxy. Do you want to know how? Keep reading!
The first thing that we need to understand is what a gravitational wave is. General Relativity, which is the most successful theory that we have nowadays to describe the gravitational interactions, accounts for the gravitational phenomena as a geometric effect. Massive objects curve space. More massive objects curve the space more: the greater the mass, the greater the curvature.

Curvature of space generated by objects of different masses.
Above this, nature is lazy. Particles always try to follow the shortest path between two points. In a curved space, the shortest path connecting two points is no longer a straight line but what we call a geodesic. For example, the earth follows an elliptic orbit around the sun due to the curvature that the sun generates in space.

Representation of the space around a large object and how it will influence the movement of a smaller object.
Yes, the earth is (almost) spherical and it describes elliptic orbits around the sun, not the other way around. I know that everyone knows this, but just in case… Anyway, coming back to our aim: what are then gravitational waves? When objects are motionless, they produce a curvature in space that is constant in time. However, objects in motion produce a curvature of space that changes with time and they can actually generate a “wiggling” of space that propagates as a wave. It might be hard to imagine, but it is space itself that is vibrating. This is what we understand as gravitational waves. The effect of gravitational waves emitted by ordinary objects like stars or planets is really tiny. However, the gravitational waves emitted by the collisions of very massive objects like two black holes can be very energetic. For example, the energy emitted per unit time by the merger of two black holes of around thirty solar masses is ten thousand times greater than the one emitted by all of the stars in all the galaxies of the observable universe. This is quite a lot!
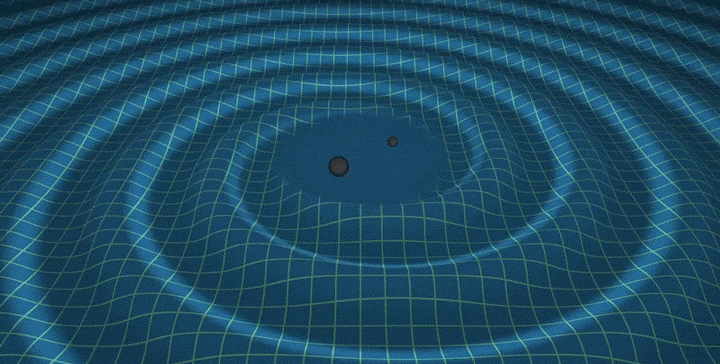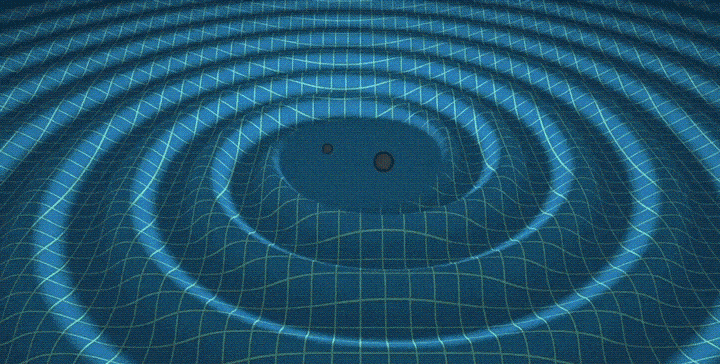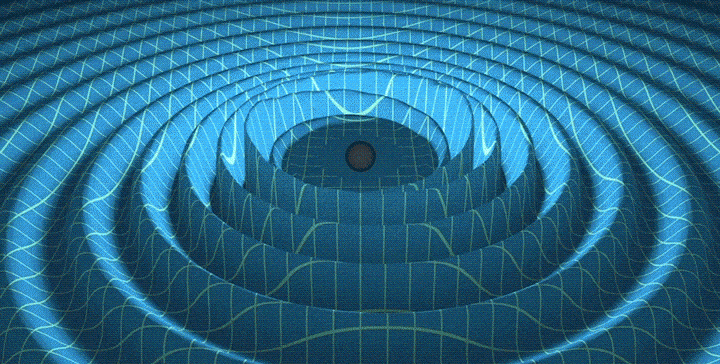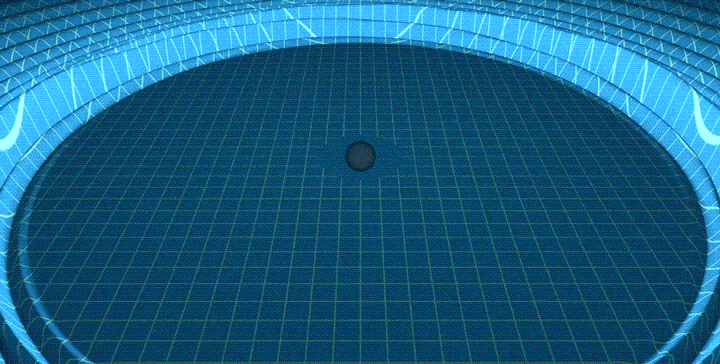
Representation of a gravitational wave created by a merger of two black holes.
As electromagnetic waves, gravitational waves are characterized by their wavelength, namely the distance between two peaks of maximum amplitude of the wave. Depending on the masses of the merging black holes, they generate gravitational waves of different wavelengths. From earth, we are able to detect gravitational waves with wavelengths comparable to the radius of the earth itself, which is around 6000 km. This is the characteristic wavelength of the gravitational waves emitted by “small” black holes (the size of a few solar masses). Supermassive black holes located at the centre of galaxies produce gravitational waves of a wavelength of the order of the distance between stars within our galaxy. This distance is of around a few parsecs, where a parsec is approximately 31,000,000,000,000 km. To detect waves of a given wavelength, one needs an antenna whose length is comparable to such wavelength. Hence, we would need an enormous antenna of the size of the whole galaxy to detect these gravitational waves! Yes, this is an enormous antenna! So, how did we “build” such a detector? We first need to understand what a pulsar is and how it is going to help us. Pulsars are extremely compact and rapidly rotating neutron stars, with a strong magnetic field which is misaligned with respect to the axis of rotation. This makes pulsars behave as lighthouses in the universe. This means that for pulsars, we detect a periodic pulse of light that hits us whenever the axis of the magnetic field points toward the earth.

Representation of a pulsar.
The time between two consecutive “flashes” of these objects is extremely regular. It can vary only by up to one part in a billion. Any kind of small perturbation around a pulsar can produce a significant deviation on the arrival time of the light pulse. For us, gravitational wave hunters, the interesting thing about this is that the passage of a gravitational wave could be the reason for such deviation in the expected time of arrival. In principle, if we detect a delay or an advance in the arrival time of a pulsar emission, we cannot ensure that its origin is the passage of a gravitational wave. It could be any other phenomena. In that sense, we are trying to hunt noise within noise. To do so, we look for correlations between the delays and advances of several pulsars within the galaxy. At this point, I need to explain a final technical detail: gravitational waves are quadrupolar. This means, they stretch space in one direction and contract it in the perpendicular direction. In other words, nearby pulsars or pulsars located at 180 degrees with respect to the earth will show a correlation (when one advances or delays the other will also advance or delay accordingly), whereas those located at 90 degrees will display an anticorrelation (when one advances the other delays).
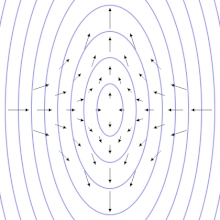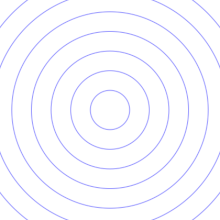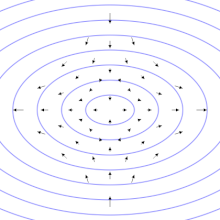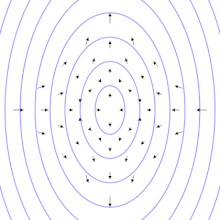
Representation of the quadrupolar characteristic of gravitational waves.
This means that within General Relativity we can compute the relative delay or advance between pulsar signals, since it only depends on their relative position in the sky and it is independent of the “intensity” of the gravitational wave passing. By intensity, I mean how much they stretch spacetime. For example, if we have two pulsars forming 90 degrees in the sky and one suffers a time delay, the other one will suffer an advance of approximately 20% of the time delay of the first one. However, to know the exact amount of delay – whether the delay is of 1s (and the advance of the other is of 0.2s) or if it is 100s (and the advance of the other is of 20s) – requires that we know the strength of the gravitational waves that are passing through the galaxy. In other words, the relative advance/delays are determined only by the passage or not of gravitational waves, but how much it is delayed depends on the intensity of the gravitational waves. To determine such intensity, we would need to track back the origin of such gravitational waves, which is not an easy task.
An analogy could serve at this point to illustrate the previous explanation. Imagine that we sit on a road just outside a car factory that produces cars of two different colours: red and blue. We know that for every red car that they produce, they also produce ten blue cars. However, it is an erratic company and it does not produce the same number of cars every day since they have very irregular suppliers of the parts they need. What we know for sure is that they always produce one red car for every ten blue cars: company’s policy. So, if we were sitting outside, we would know in advance that for every ten blue cars that pass, we would see one red car. Whether we will see twenty blue cars and two red cars, or thirty blue cars and three red cars that day requires knowledge of the supplier records. It is exactly what we experience with the pulsar time delay: we know the relative delays or advances (one red car per twenty blue cars) between pulsar signals, but how much they delay requires to know in detail the origin of the gravitational waves (how many cars will come).
The relative time advances and delays predicted by General Relativity perfectly match the observations. The interesting part comes from the observations of the exact amount of time delays and advances and their comparison with theoretical predictions. As we have discussed, to make a theoretical prediction of how much is the time advance/delay we would need to compute exactly the number of gravitational waves that are generated in the whole universe that are able to reach our galaxy. That would require to know explicitly the number of galaxies with supermassive black holes, how many mergers of two or more of such black holes have occurred in the whole history of the universe and also the number of gravitational waves generated in such events. We estimate such events with the information that we have about the history of the universe, which combines observations and models. The result of the total delay/advance of the pulsars that is obtained by computing the gravitational waves in these events is slightly below the signal detected recently by the PTA collaboration (see figure below). It might be that we are missing some black holes because there is something we do not understand well about the history of the universe. Or it might be the case that there are other sources that produce such gravitational waves, yet to be discovered! This is amazing news: gravitational waves open a new window to the universe and we might even be able to use them to discover some new astrophysical objects to which we were blind before!

Plot of the signal of gravitational waves detected experimentally. The dashed line represents the theoretical prediction based on our estimations for the number of gravitational waves that we expect and it is slightly below the observations.
