Quantum vacuum: the cosmological constant problem

(A desperate attempt at explaining infinity in finite terms…)

1 Einstein and the cosmological constant

I invite the nonexpert reader to a short but intense incursion into the jungle of the quantum vacuum and to meet there the fiercest and most famous theoretical conundrum of all times: “the cosmological constant problem” (CCP). For more than a century (since 1917) we have heard of the cosmological constant in Einstein’s field equations, the parameter that we usually indicate as Λ but Einstein denoted λ (in lower case)¹. The gravitational field equations had been introduced by him a couple of years before without such a term. But at that time the stars in the firmament were thought to be fixed and this spread the (wrong) idea that the Cosmos was static. A positive cosmological term (Λ > 0) can produce the desired effect, in principle, namely of having a static Cosmos in which there is a perfect balance between the gravitational pull of matter and the negative pressure produced by a (positive) cosmological term – effectively acting as a kind of antigravitational force. Einstein introduced that term in his equations upon realizing that it did not destroy the general covariance (…”ohne daß dadurch die allgemeine Kovarianz zerstört wird.” [1]) of General Relativity (GR), which is the fundamental paradigm on which GR is built upon.

At that time he did not know that a static Universe balanced with such a term was actually in a precarious state of unstable equilibrium (the slightest unbalance between the two antagonistic forces would cause a runaway motion of the Universe into expansion or collapse!), but it served his purpose for a while. Of course, we now know that the Cosmos is not static, and in fact a few years after Einstein had introduced the cosmological term, Hubble’s observations convinced the scientific community that the Universe is expanding. In view of this empirical fact, Einstein decided to abandon the Λ-term [2], despite its presence in no way contradicts the expansion of the Universe! But he thought that the additional parameter Λ could be spared, to the point that in 1932 he wrote a paper together with his colleague W. de Sitter proposing a cosmological model of the Universe (the so-called ‘Einstein de Sitter model’) where Λ was banished altogether![3]. Unfortunately, in doing so he forgot the famous saying: “once you let the genie out of the bottle, there is no possible way you can put it back!” Namely, once you recognize that the Λ-term is compatible with the GR paradigm, as Einstein himself remarked, there is no possibility to withdraw it, meaning that one cannot undo that action anymore and set Λ = 0 back for free. In truth, 50 years after having been introduced, in 1967, the famous Russian physicist Yakov Zeldovich pointed out [4] that even if you set Λ = 0 at the classical level, quantum theory enforces Λ ≠ 0 again! The idea was reminiscent of Planck’s ‘Nullpunktsenergie’ (zero-point energy – ZPE) in the context of his studies on the spectrum of the thermal black-body radiation. Each oscillation mode contributes the famous energy amount E_k = ½ ħω_k, where ħ is Planck’s constant and ω_k is the frequency of the kth oscillation mode. Zeldovich went beyond Planck in that he made the point that all of the quantum fields (not just the electromagnetic field) fluctuate in the vacuum and therefore induce a ZPE. Even more, he contended that the continuous fluctuations of vacuum (see Fig. 1) induce an inordinately large value (formally infinite) of the vacuum energy density ρ_vac, and hence of the cosmological constant as well, since they are just proportional: ρ_vac= Λ/(8πG_N), with G_N being Newton’s constant. More specifically, Zeldovich argued on the basis of simple dimensional analysis that the induced ZPE value, upon subtracting (“renormalizing”) the infinite contribution, must be proportional to the quartic power of the masses of the quantum fields, a result that we may roughly indicated as ZPE∼ m⁴.  For most of the known elementary particles (except for a very light neutrino), the corresponding renormalized ZPE proves to be many orders of magnitude larger than the measured value of Λ from observations, a fact which is of course rather disappointing if there is to be a connection between the quantum vacuum and the cosmic vacuum.

As we know, the value of Λ has been measured using Type Ia supernovae data since 1998-99 (by independent astrophysicists teams led by A. Riess and S. Perlmutter), and subsequently it has been cross-checked with alternative measurements based on cosmic microwave background (CMB) and baryonic acoustic oscillations (BAO) data. The remarkably good agreement between the variety of measurements of Λ confirmed that the observed value is incommensurably much smaller than the theoretically predicted one within quantum field theory (QFT). Of course, this is telling us that we are facing at this point a phenomenal theoretical conundrum, which cries out for a solution on fundamental grounds – not just from empirical considerations, as otherwise we lose all hopes to eventually understand cosmology using the same scientific paradigms with which we understand quantum physics and elementary particles. Notwithstanding, if we leave this terrible setback aside for a moment, the fact that the observed value of the cosmological term is positive, Λ > 0, demonstrates another important thing, to wit: the expansion of the Universe is accelerated! In other words, the Cosmos evolution is speeding up and so its expansion rate H(t) (the instantaneous ‘Hubble parameter’) tends to increase rather than decrease with the cosmic time t. If Einstein would have not dismissed Λ, fourteen years after he had introduced it, he could have predicted the acceleration of the cosmic expansion! Therefore, his legendary comment “…was the biggest blunder of my life” (as he called his proposal on the Λ-term, according to George Gamow’s autobiography[5]) proved to be actually a double blunder when he finally repudiated Λ!

2 Our beloved ΛCDM

The present situation is that the rejected Λ-term by Einstein is fully back in our basic cosmological equations and, as previously emphasized, it has been measured to be nonzero and positive with fantastic precision. Thus Λ has become part of what we call the ΛCDM model, namely the standard (or ‘concordance’) model of cosmology. The latter includes also the hypothesis of ‘dark matter’ (DM), motivated by our (empirical) knowledge that most of the matter that we  need in order  to explain the observations cannot just be the very same ordinary stuff of which we are made (protons, neutrons and electrons). This fact has been known for a long time and rests heavily upon our understanding of the Big Bang Nucleosynthesis of the primordial elements (hydrogen, helium, lithium, etc.). Unfortunately, the nature of the DM still escapes our control, as no dark matter particle has ever been observed in a direct way, and therefore this also causes big concern as to the viability of the assumptions involved in the ΛCDM structure. Not surprisingly, the DM story is a no less thrilling – and yet no less frustrating – chapter of the cosmic drama. But at this point I must entirely skip it since I need to come back to the cosmological constant problem and also to something really weird, but closely related to it, which is called ‘dark energy’ (DE).

Phenomenologically, the concordance ΛCDM model fares quite well in general, which means that if we accept that there is some form of DM out there (to be discovered some day perhaps) and that the parameter Λ is all that we need to explain the cosmic acceleration, then many other things can be deemed to be pretty well under control. However,  it is only a partial success, of course.  If we pay attention to the existing conflicts on several active fronts, the observational situation of the ΛCDM in the last decade or so does not seem to paint a fully rosy picture anymore. Beyond formal theoretical issues that have been dragged along for more than half a century, such as the aforementioned CCP (see below for more discussion on it), a series of practical problems of more mundane nature are piling up in the backyard of the standard model. On a mere phenomenological perspective, it is particularly worrisome the situation with some “tensions” existing with the data [6]. For example, it has long been known that there appear to exist potentially serious disagreements between the CMB observations and the local direct (distance ladder) measurements of the Hubble parameter today. The persisting mismatch between these measurements is what has been called the “H₀-tension”. It is arguably the most puzzling open question within the current cosmological paradigm and it leads, if taken at face value, to a severe inconsistency of ∼ 5σ c.l.  or more, between the mentioned observables.  Another difficulty resides in the  matter clustering parameter σ₈, and is called the “σ₈-tension”, related with the exceeding rate of large scale structure formation predicted by the ΛCDM as compared to measurements, although the discordance here is a more moderate one, at the ∼ 2 − 3σ level.  Many cosmologists intend to tackle these discrepancies by looking for systematic errors. The bare truth, however, is that the radical simplicity of the ΛCDM model leaves little room for a sound explanation of these tensions beyond methodological issues related with observations. The absence of any obvious connection of the model with the fundamental physical interactions (apart from gravity) is quite likely the cause of the main inconsistencies. The ΛCDM does not possess enough theoretical structure neither to explain the successfulness of the observations (e.g. to understand what is the measured value of Λ on a fundamental context), nor to account for the troubles threatening its viability. The million-dollar question is now the following: is it possible to solve those lingering ‘petty’ issues by solving the biggest issue of all? The answer is not obvious, but the question is at least perfectly licit. And it is so because the solution of the CCP might require a change of paradigm: Λ is most likely not constant. And this could impinge on the remaining problems, of course.

3 Fine tuning nightmare

While the measurement of the value of Λ is a spectacular triumph of observational cosmology, the ‘explanation’ of the cosmic acceleration based on that measurement is in no way satisfactory from a theoretical point of view, for it clashes violently with the predictions from fundamental physics (such as quantum field theory and string theory). Or just to be phrased the other way around: theoretical ideas blatantly fail to describe the direct observations on Λ! Be as it may, let us now come to grips with the main issue: what is the CCP in more specific terms? We must come back to Zeldovich’s insightful remark, and even dare go beyond it.  It turns out that the measured Λ  is at least 55 orders of magnitude smaller than the value predicted within the Standard Model of the strong and electroweak interactions. In point of fact, every quantum field fluctuating in the vacuum, whether boson or fermion, generates a ‘zero-point energy’, as indicated above, and such a ZPE makes the value of Λ many orders of magnitude larger than the measured parameter. The CCP acquires its frantic peak of severity if taking into account the vacuum contribution from the Grand Unified Theories or even the Planck scale (the putative ‘anteroom’ of quantum gravity), as in that case the disagreement is more than 120 orders of magnitude (viz. ‘1’ followed by 120 zeros). This is, of course, insane! But there is no need to go that far: the CCP, if restricted only to the domain of the standard model of particle physics, is already sufficiently severe as to be taken fully in earnest. After all particle physics is a very serious matter, as it represents the state-of-the-art of precision science! So, those devastating 55 orders of magnitude of difference are there, and they are more than enough to make our lives a true ordeal. Unless there is a mysterious cancellation among all the individual contributions (bosons contribute positive sign and fermions negative sign), there is no way to get rid of a huge prediction for Λ which we do not observe at all! The necessity for such a cancellation among all of the large contributions in order to obtain a result much smaller than each individual term is called the ‘fine tuning problem’. It is at the very hardcore of the CCP. Regrettably, there is no obvious reason for obtaining a coincidental cancellation among all these unbridled incomes of quantum energy with different signs. The sought-for magics is not even possible in supersymmetric theories, which postulate the same number of bosons and fermion degrees of freedom – contributing with opposite signs to the vacuum reservoir. The reason is that supersymmetry is not a real symmetry in the present Universe, it is at best a broken one. It might have been a symmetry of the early Universe, but not now, so it does not help at all in this business despite naive expectations.

All in all, we do not seem to have at present any natural solution to the fine tuning nightmare, and this failure proves to be a major stumbling block to our understanding of cosmology from first principles. This is at least what the standard lore on the subject has been repeating once and again as of the time Zeldovich made his point on the ZPE, which if taken at face value may seriously jeopardize the possibility that the quantum vacuum can be a reasonable explanation for the Λ term in Einstein’s equations. The abhorrent mismatch which is involved between theory and observation in the realm of cosmology when we try to make sense of the value of Λ constitutes the very embodiment of the so-called ‘old’ cosmological constant problem (CCP). It has been recognized as the most challenging conundrum of theoretical physics and cosmology ever, see e.g. [7, 8, 9, 10, 11] for reviews. For nearly 60 years the CCP has been the main source of headache for every theoretical cosmologist confronting his/her models with the observed value of Λ. Not to mention that it has been a relentless flashpoint of tension with particle physics, this still being true at present. In fact, the discovery in 2012 of the Higgs boson at the LHC accelerator at CERN has accentuated the CCP to the utmost, certainly much more than is usually recognized. While Zeldovich’s observation referred to the zero-point energies of all the quantum fields, including the Higgs boson, this particle adds up still one more independent contribution (call it ρ_{vac Higgs}, see Fig. 2) to the vacuum energy which further aggravates the CCP. It stems from the electroweak interactions and is given by the value V_Higgs of the Higgs potential at its ground state. Indeed, owing to the necessary spontaneous symmetry breaking (SSB) of the electroweak (EW) theory – through the so-called Higgs mechanism – it turns out that an induced effect on Λ is also generated from the EW vacuum, which is appallingly much larger (a factor ∼ 10⁵⁵: ‘1’ followed by 55 zeros!) than the tiny value of the vacuum energy density associated to the cosmological term: ρ_vac ∼ 10⁻⁴⁷ GeV⁴, in particle physics units ². So the world-wide celebrated “success” about the Higgs discovery at CERN, made twelve years ago, actually became a colossal fiasco from the viewpoint of cosmology, as it instantly detonated the “modern CCP”, i.e. the confirmation about the gruelling value of the EW vacuum energy density, whose existence adds up more drama to the CCP. If the Higgs boson has been found, the EW vacuum energy should be considered as real as the Higgs boson itself!

With this gloomy state of affairs, we find ourselves in a rather uncomfortable situation. For we have a so-called standard cosmological model, the ΛCDM, which does fairly well phenomeno- logically but remains in limbo, deprived from the necessary theoretical underpinning. The Λ-term in it, for example, is a mere fitting parameter, nothing else. The fact that we have measured it with quite some precision does not mean we have understood an inch about its meaning! The ΛCDM is certainly related with GR, but its basic parameters seem not to have any explanation in the framework of particle physics or quantum field theory. Not surprisingly, particle physics is at odds with cosmology at the fundamental theoretical level. Put another way, the Microcosmos seems to be entirely divorced from the Macrocosmos, which is a real tragedy for getting a chance at an overarching vision and at a profound understanding of the Universe from first principles.

4 Quintessence, phantom and all that

It is in part for this reason that some ersatz for Λ was finally concocted. At the end of the eighties, and also at the end of the nineties, two independent waves of theoretical cosmologists thought on possible alternatives to the quantum vacuum as a source of the cosmological term. The denomination ‘quintessence’ was coined to represent a dynamical scalar field (φ) evolving with the expansion and whose potential energy at present would supplant the value of Λ. The idea is partly fruitful in that it offers a simple scenario for performing field theory calculations, but it is a bit misleading since it replaces all of a sudden the quantum vacuum (a firm prediction of the successful quantum field theory describing quarks, leptons, gauge bosons and the Higgs particle) with new and totally ad hoc fields, which are actually classical (not quantum) and were introduced with the sole purpose of describing the value of the cosmological term Λ without making reference to quantum theory. Obviously, proceeding this way is tantamount to putting aside all that we know about the standard model of particle physics (that is to say, the fundamental theory of the strong and electroweak interactions) and start playing around with the new stuff without even having  a  minimally  credible  framework  that  can  provide  a  raison  d’être  for  the  existence  of  the newly invented fields. Besides, this does not solve the CCP either, as the fine tuning problem is still there in its full glory. In fact, Λ, or, more precisely, ρ_vac = Λ/(8πG_N ), is now superseded by the ground state value of some potential V (φ). There is, however, no obvious reason for such a potential to take on precisely the tiny Λ value measured at present. This is only possible if we could understand the dynamics of φ in the context of a much wider picture, which is however not provided. One may think of φ as some scalar field pertaining to a Grand Unified Theory (GUT), e.g. a field which is still surviving at present as a kind of fossil of the early Universe. But this idea was never substantiated with the necessary details to make it sufficiently plausible. It nevertheless entails an appealing feature in that φ = φ(t) is dynamical, i.e. it evolves with the cosmic time t, and hence the predicted value of V (φ(t)) is also evolving with the expansion. One hopes that this can help solving the ‘cosmic coincidence problem’, namely why the value of the energy density associated to Λ is so close to the current value of the matter density. If the latter evolves continuously with the expansion while Λ doesn’t, there is no chance for understanding such a cosmic coincidence, but if both quantities are dynamical the coincidence is more likely, especially if the dynamics is guided by fixed points of the cosmic evolution, presumably encoded in some forms of the potential V (φ). However, despite much work in this direction over the years, the quintessence approach has never been able to explain the value of Λ and, above all, it did  not explain in a minimally convincing way why we can address the cosmological problems of our Universe as if the quantum vacuum would not be there at all, namely as if we could put quantum theory under the rug and ignore it altogether in all cosmological considerations.

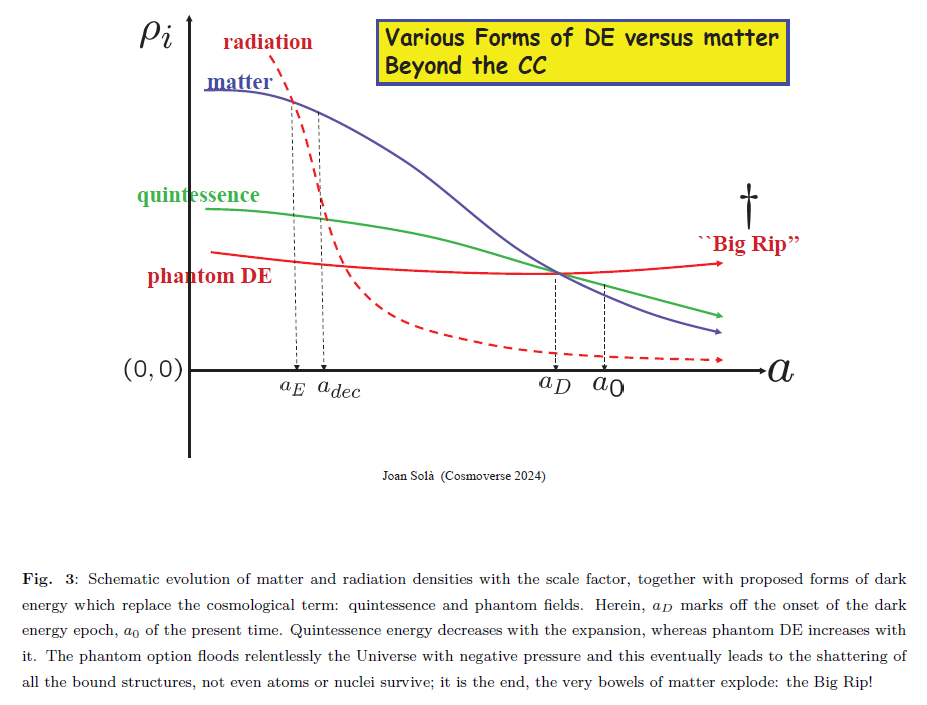
The CCP is indeed such a tough problem that people somehow decided to put this nightmare to the back of their minds and preferred to search desperately in other directions. In point of fact, the searching ‘paroxysm’ about finding substitutes for the “troublesome” quantum vacuum did not stop with quintessence. Soon a new generation of mysterious scalar fields called “phantom fields” started to circulate in the scientific literature. A phantom field is just like a quintessence field, except that its energy density increases with the expansion (in contrast to quintessence, whose energy decreases with time, see Fig. 3). In addition, the negative cosmic pressure produced by a phantom field surpasses that of the Λ term in absolute value (while quintessence gives a milder negative pressure than the vacuum). The outcome is that the phantom dominated Universe will be eventually torn into pieces since all bound states will become disrupted by the evermore increasing negative pressure. No form of matter can survive; not only planets and galaxies are to be destroyed mercilessly but also all atoms, even the protons. The final stage of such a catastrophic doomsday is called the ‘Big Rip’, as every piece of matter will be ripped out – virtually exploding on account of the unbearable negative pressure. Despite it being a very sad end for the Universe, some cosmologists dare using the idea because there is no harm at present (we are still far away from the hypothetical Big Rip) and in the meantime phantom fields can help to alleviate those pressing tensions in the cosmological observations. Phantom fields, however, are just the tip of the iceberg of a large body of exotic ideas on how to explain the acceleration of the Universe without invoking the Λ term and the quantum vacuum energy ρ_vac. The appeal to the “DE box” has become now quite common among theoretical cosmologists. Whenever we have some bothersome tension in cosmology which we cannot account within the concordance model ΛCDM, we routinely start shaking hard that tool box of the DE, which is full of toys and trickeries accumulated over time, and we try to find one piece that can fit our purposes, or just invent a brand new one!

Another possibility to sort out the quantum vacuum is to abandon the idea that gravity is a fundamental interaction. Some people actually believe that gravity is an ‘emergent’ (or entropic) phenomenon, whose fundamental degrees of freedom have not been identified yet. For example, before Boltzmann introduced Statistical Mechanics, the phenomena involving conversions of work into heat and vice versa were described by an effective theory that we call thermodynamics. It deals with macroscopic quantities such as pressure, volume, temperature and entropy without even assuming the existence of ordinary microscopic degrees of freedom like atoms and molecules. So if gravity is also a sort of thermodynamical notion which is blind to some purported fundamental degrees of freedom, then the existence of quantum gravity is not warranted. We cannot exclude anything at this point, but other possibilities are still available before we give up in our efforts to connect gravity with the quantum world. Worth noticing is also the approach to the CCP called the ‘Anthropic Principle’, which is an attempt based on using the existence of life and the human being in the Universe. Steven Weinberg and collaborators proposed the idea in 1997, as a method to estimate the maximum size which Λ can attain to be compatible with the existence of standard galaxies that can welcome life. The idea is interesting, but life and even humans play again a too central role in the story, and so it is usually not considered a formal solution to the CCP.

5 Zero-point energy of quantum fields in curved spacetime

In my CosmoVerse seminar on February 21th, 2024, entitled “Running vacuum in the Universe: theoretical framework and implications on the cosmological problems and tensions” – which has primarily motivated this article for a wider audience – I have tried to show that the CCP can actually be alleviated and that the quantum vacuum is not such an insurmountable obstacle if one deals with it appropriately in the context of quantum field theory (QFT) in curved spacetime. The technical details given in my talk are not to be repeated here, of course, see for example [10] for a recent review, and particularly [11] for more readable accounts including some historical notes and bibliography. Still, some simple explanations can be provided now which will suffice for most readers. Recall that a critical issue involved in the CCP described above is that there are many large particle physics contributions to the vacuum energy ρ_vac, and hence to Λ, which altogether should – almost – cancel out and leave a tiny remainder, namely one which can be amenable to the cosmological context (see the last footnote). To start with, the sum over all frequency modes of the vacuum fluctuations (see Fig. 1) becomes a badly divergent integral:

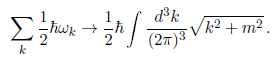
This integral is nothing but the aforementioned ZPE and it depends on the mass m of the quantum field. Following Zeldovich’s insight, we should expect that it will render a quartic power of the mass (∼ m⁴) – as can be suspected on dimensional grounds. However, as warned, the integral is divergent, so something must be done before attaining that (finite) result.  Furthermore, the previous form of the ZPE applies only to flat (Minkowski) spacetime, not to cosmological spacetime (viz.  Friedmann-Lemaˆıtre-Robertson-Walker spacetime). The latter is curved, and the spacetime curvature R is roughly proportional to the square of the Hubble rate:  R ∼ H².  But there is no trace whatsoever of curvature in that ZPE formula, isn’t it? Can you see any dependence on the Hubble rate H in it? I can’t! So away with that formula, it cannot represent the vacuum energy in our real Universe. In curved spacetime, however, the frequency modes ω_k depend on the geometry of spacetime. So, we expect that the suitable ZPE-integral should depend on the curvature R, and hence on H². This proves correct and is very important. We need not disclose the complicated details here [12]. It is amazing to see, though, so many calculations in the literature about renormalizing the vacuum energy based on just Minkowski spacetime considerations, i.e. on just the above integral. This is simply nonsense. The calculation must be performed in cosmological spacetime, it is a must. But even this is not enough, remember that the integral is infinite and hence we must ‘extract’ the infinity of that integral before interpreting the final result. Now whenever we meet a divergent integral in QFT, we say that ‘renormalization’ is required, which is an educated prescription for subtracting infinities and leave finite (renormalized) quantities: these are the observable results which might finally be subject to measurement. However, renormalization is a rather subtle technique in QFT and not all renormalization schemes lead to the physical results in a transparent way. In addition, it is a mathematical procedure which in many cases is rather blind to physical considerations, and our duty as physicists is to use an approach that is as close as possible to physics. The very understanding of the CCP depends on this crucial fact!

6 The riddle of how infinity is traded for a conspiracy of finites!

Infinities are not easy to handle, even after renormalization takes care of them. But renormalization does not always provide a direct contact with the physical quantities. Sometimes this last step can be the most challenging one, even more than dealing with the infinities themselves. In truth, the vacuum energy in cosmology is a unique arena where after getting rid of the infinities we are left with a ‘conspiracy’ of finite quantities which are incommensurably much larger than any cosmological observable of the present Universe. Let us first recall that the vacuum energy density is not just the usual constant term ρ_Λ in Einstein equations. This is only true at the classical level. In the quantum field theory context, Zeldovich told us that we have still to add the zero- point energy of all the quantum fields, and then perform renormalization (since, as you know, the ZPE is infinite – see Fig. 1).  Hence the vacuum  energy density reads:  ρ_vac  = ρ_Λ + ZPE.  The  last piece (a pure quantum effect) is the truly problematic one, but also the clue to the enigma. Indeed, what happens when the ZPE-integral is renormalized? In most renormalization schemes, once the infinity has been removed, the final result is some expression which is proportional to the mentioned quartic power of the mass, ∼ m⁴, as predicted by Zeldovich. Since, however, the mass scales of all known particles in the standard model of particle physics are very large as compared to any cosmological energy scale at present (with the exception of a very light neutrino of order of a mili-electronvolt), each individual particle contribution ∼ m⁴ is always far too big and, as warned previously, there does not seem to exist any viable mechanism (not even supersymmetry) that can be made to work in the current Universe, namely one which is capable of magically combining all these individual contributions m₁⁴ – m₂⁴ + m₃⁴ – … (some with different signs) to yield a net final result which is much smaller than each of the m⁴ contributions in isolation.  For the sake of simplicity, let us take just one single particle, say the Higgs boson, with a measured mass of about M_H = 125 GeV. Following Zeldovich’s recipe, its contribution to the ZPE must be of order 125⁴ = 244, 140, 625 (in GeV⁴ units for all these numerical considerations). Thus, as previously indicated, the sum of this contribution plus the ρ_Λ term in Einstein’s equations must give the measured value of the vacuum energy density, ρ_vac, which is comparatively much smaller (of order 10⁻⁴⁷ GeV⁴, see the last footnote). Thus,

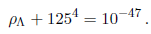
This equation determines ρ_Λ, but if you think twice about it, it proves quite odd! After a bit of reasoning, you will quickly convince yourself that the value of ρ_Λ solving that equation must be chosen with such a fantastic precision (fine tuned!) as to be almost exactly equal to (and with opposite sign to) the very large number 125⁴, specifically to within an accuracy of 55 digits! This is precisely the magnitude of the adjustment to be made owing to the Higgs input to the ZPE (plus the aforementioned electroweak contribution of the same order from the Higgs potential, which is absolutely necessary to give masses to all the particles of the standard model, cf. Fig. 2)³. Needles to say, we cannot buy this ‘solution’ to the CCP, as this is no solution at all but sheer madness. Such a preposterous result shows rather convincingly how unnatural it would be to admit the existence of a ‘fine tuning’ mechanism capable of performing the required adjustment. This is why the CCP is usually considered as the toughest theoretical riddle of all physics! It is also, most likely, the reason why we usually conceive the CCP as if it were just some extremely extravagant puzzle of pure theoretical nature with no practical interest. We simply close our eyes to that repulsive creature and focus exclusively on the ‘standard’ cosmological tensions (H₀, σ₈,…). In doing this we are forgetting perhaps that the ‘extravagant’ and the ‘real’ sometimes might have some intimate and surprising connection. In the following I’ll try to argue that the possible connection leads to a Λ-term which is actually not constant, but running with the cosmic accelerated expansion.

7 Running Vacuum in the expanding Universe

The CCP is such an excruciating enigma that we tend to apply the ‘ostrich-like technique’ of burying our heads in the sand not to see it, but it doesn’t help much since the CCP is still there, as defiant as always, and it will not disappear into thin air only because we stop looking at it. The origin of that baffling and distressing situation stems from the extremely large ∼ m⁴ effects foreseen by Zeldovich (Fig. 1). But now a truly unfathomable surprise emerges as though a revelation: after all the fuss, those terms are actually not there! – at least not in the final result! In fact, appropriate renormalization within the running vacuum framework [10] shows that the vacuum energy density can be brought into compliance with the cosmological standards and appear as a smooth function of the Hubble rate, ρ_vac = ρ_vac(H). How it works? Mind what we said before about the ZPE in curved spacetime: it is a function of curvature and hence of the square of the Hubble rate. Still, the ZPE is a divergent quantity and for a proper interpretation we must first get rid of the infinite term carried by it, i.e. we need to renormalize the ZPE. This can be properly achieved by subtracting the value of the vacuum energy density, ρ_vac, between any two points of the cosmic evolution characterized by different values of the Hubble scale, say H₀ (the current value) and H (e.g. some other value lying in our recent past). Recall that ρ_vac = ρ_Λ + ZPE,  so when we perform the mentioned subtraction both terms, ρ_Λ and ZPE, obviously participate in the difference between the two H-scales. At this juncture a marvelous cancellation occurs between the troublesome ∼ m⁴ terms carried along by both ρ_Λ and ZPE separately, leaving as a net result only a very smooth function of the Hubble rate (specifically, a series of powers of H and its time derivatives). Detailed calculations [12] indeed confirm that in performing such a subtraction, not only the infinities cancel out, but also the onerous finite terms ∼ m⁴ from all sorts of massive particles, which otherwise would lead to the mentioned fine tuning madness. Amazingly enough, our nightmare somehow vanished magically in a twinkle of an eye! The offending quartic powers ∼ m⁴ predicted by Zeldovich just disappeared from the final result: those encoded in ρ_Λ just cancel against those embodied in the ZPE, leaving a residue of order ∼ m²H², hence much-much smaller than m⁴! A miracle? Not at all, it was probably the right thing to do, that is to say, the ‘correct’ renormalization procedure: the physical one! The outcome is that any two nearby points of the cosmic evolution are smoothly related by a vacuum energy difference of order H², with no trace left of ∼ m⁴ terms, and hence no fine tuning is needed at all.  Formally, we say that the quantum scaling of ρ_vac with the renormalization point (H) turned into cosmic evolution with the Hubble rate⁴.  Thus,  QFT tells us that what we  call the ‘cosmological constant’ Λ is like a ‘mirage’,  it     is not constant at all; it is the nearly sustained value of ρ_vac(H) around any given cosmic epoch. Remember that ρ_vac and Λ are proportional. Therefore Λ itself is a function of the cosmic epoch, Λ = Λ(H); so when we move from one epoch (H₀) to another (H) we can determine Λ(H) from Λ(H₀) by adding a difference Λ(H)−Λ(H₀) to the latter which is free from the troublesome quartic mass terms ∼ m⁴ for only powers of H remain, these being no larger than the critical density now. The difference of vacuum energy densities between any two cosmic epochs is, therefore, in perfect agreement with observation. There is no need at all for fine tuning since the cosmological ‘constant’ Λ(H) remains ∼ H² at all times. The renormalization framework of the vacuum energy with such remarkable properties is called the ‘Running Vacuum Model (RVM)’[10] .

The upshot of this cosmic drama (which was on the verge of becoming a tragedy!) is that notwithstanding all of the evils uttered against the quantum vacuum for being plagued with the cosmological constant problem, it is not so, just the very opposite: the quantum vacuum behaves smoothly and it constitutes the real (physical) cause of the speeding up of the Universe, a fact that can be bolstered in the context of fundamental physics, such as quantum field theory and even string theory [12, 13]. No need to invoke toy models based on ad hoc fields being artificially introduced for this sole purpose. Even if these fields might be there, they are not an ersatz for the quantum vacuum. At the end of the day, there is no more trouble associated to the quantum vacuum than there is for any of the trickeries that we hide in the tool box of the DE. With one big difference, though: the quantum vacuum is no trick at all.  Why such a fuss, then, with Λ  and the CCP? Attempts to get rid of infinities associated with the renormalization of the vacuum energy in curved spacetime as if it were flat (Minkowski) spacetime, together with an incorrect identification of the renormalization scale (which should be the Hubble rate and no other) has prolonged the agony of the CCP to our days. My own understanding of the CCP is that it is an ill formulated theoretical problem. Rather than to blame quantum theory as the underlying cause of the CCP, it is actually its solution! Furthermore, the running vacuum framework has not only a nontrivial impact on the CCP, which in itself is probably the major issue; it also has a positive bearing on the current practical hitches, such as the H₀ and σ₈ tensions.  This is demonstrated  in a number of phenomenological analyses, in which the RVM is confronted successfully with the wealth of cosmological data, as can be seen in the recent studies [14] and references therein.

To summarize, because of inappropriate renormalization schemes, for a long time we have been tripped up in formal issues and we have deluded ourselves into believing that we are forced to perform unnatural fine tuning of the parameters in the computation of the vacuum energy density (VED) owing to the presence of the Zeldovich kind of ∼ m⁴ terms. The RVM approach [12], however, gets rid of them all in the physical result and leaves a commensurable vacuum energy which is in perfect accord with the cosmological scales rather than being light years from them!

8 Quantum vacuum: the biggest cosmic chameleon

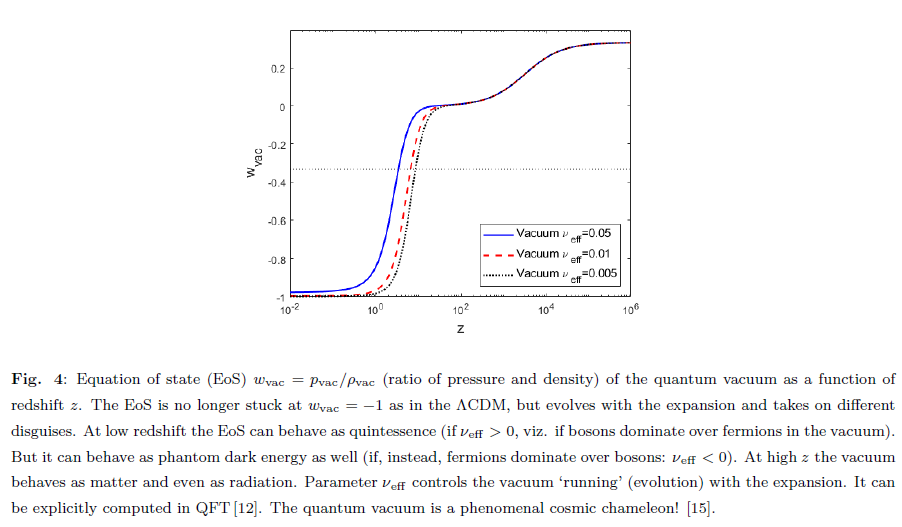
As a smoking gun of this novel renormalization framework of the vacuum energy in cosmology, we are left with a very useful signature (Fig. 4), to wit: the equation of state (EoS) of the quantum vacuum is no longer stuck at the rigid value −1. It proves to be dynamical, and it mimics quintessence or phantom DE at small redshift (depending on whether the running of the vacuum is dominated by the positive contributions from bosons or the negative contributions from fermions). We cannot know a priori which one is the predominant contribution, it must be decided from cosmological observation. However, the RVM framework provides a specific link between fundamental physics and effective cosmologic behaviors which were (and are) too often attributed to different kinds of stunts being kept in the tool box of the dark energy. There is therefore no a priori need for ‘real” quintessence or phantom fields. The quantum vacuum does itself automatically the fine job (cf. Fig. 4): it appears sometimes as classic vacuum (during inflation, where we have w_vac = −1 exactly), some other times appears as matter (w_vac = 0) or radiation (w_vac = 1/3), and even dares dressing-up as quintessence (w_vac > −1) and phantom dark energy (w_vac < −1). The quantum vacuum is the biggest cosmic chameleon of all! [15]. Needless to say, more work will be necessary in the future to further substantiate these phenomenological and theoretical aspects of the quantum vacuum, and especially in what concerns the contributions from spontaneous symmetry breaking such as the Higgs mechanism, as these quantum effects are even more complicated to deal with than the zero-point energies of the quantum fields. In the light of these studies, however, one purely theoretical result stands out which cannot be overemphasized and no longer stays at the mercy of the whims of the observations (often subdued to changes and vicissitudes over time), namely the fact that if the quantum vacuum bears relation with – or is even precisely identified with – the cosmic vacuum, then Λ cannot be anymore an immutable constant throughout the cosmic history.

Notes:

¹“Wir können nämlich auf der linken Seite der Feldgleichungen [(13)] den mit einer vorläufig unbekannten universellen Konstante –λ  multiplizierten Fundamentaltensor g_µν  hinzufügen, ..” (A. Einstein [1])

²Here “tiny” only means within the particle physics standards, of course. The value ρvac  ∼ 10⁻⁴⁷ GeV⁴ is just of the order of the current critical density, ρc ∼ 10⁻²⁹ g/cm³ (if expressed in more conventional units), hence a pretty normal value in the cosmological arena. Nevertheless, what appears to be a ‘normal’ scale in cosmology may not appear normal at all in the particle physics domain, and vice versa. This is at the root of the CCP problem!

³ The attentive reader may have noticed that in the case of the Higgs particle, the ZPE contribution ∼ M_H⁴ and the electroweak vacuum energy |VHiggs| ∼ M_H²Hυ² generated by the Higgs mechanism (see Fig. 2) are both of the same order of magnitude ∼ 10⁸ GeV⁴ and both entail a bulk tension of about 55 orders of magnitude with respect to the observed value ρ_vac ∼ 10⁻⁴⁷ GeV⁴. This is, however, coincidental and stems from the fact that the Higgs mass, which is not predicted at all by the standard model of particle physics (it was just measured experimentally in 2012), turns out to be not far away from the vacuum expectation value of the Higgs field, M_H ∼ υ, and hence |VHiggs| ∼ M_H⁴ (in order of magnitude) . While the two contributions M_H⁴  and V_Higgs are similar and have actually opposite signs (see again Fig. 2), they do not cancel. So, the problem remains intact since the difference between two unrelated numbers leading each to a mind-boggling 10⁵⁵ discrepancy is again another mind-boggling 10⁵⁵ discrepancy!

⁴ The procedure is actually not very different from what is usually done, say, in quantum electrodynamics and other gauge theories in particle physics, where the gauge coupling becomes a function of the renormalization point and then we choose this point at a characteristic energy of the physical process. In the cosmic playground the ‘characteristic energy scale’ is provided by the value of the Hubble rate at each stage of the cosmic evolution.

References

[1] A.  Einstein,  Kosmologische Betrachtungen zur allgemeinen Relativit¨atstheorie,  Sitzungsber. K¨onigl. Preuss. Akad. Wiss. phys.-math. Klasse VI (1917) 142.

[2] A.  Einstein,  Zum kosmologischen Problem der allgemeinen Relativita¨tstheorie,  Sitzungsber. K¨onigl. Preuss. Akad. Wiss. phys.-math. Klasse XII, (1931) 235.

[3] A. Einstein and W. de Sitter, On the Relation between the Expansion and the Mean Density of the Universe, Proc.Nat.Acad.Sci. 18 (1932) 213.

[4] Y.B. Zeldovich, Cosmological constant and elementary particles, JETP Lett. 6 (1967) 316; Pisma Zh. Eksp. Teor. Fiz., 6 (1967) 883.

[5] G. Gamow, My World Line, The Viking Press, New York, (1970) – see particularly p. 44.

[6] Abdalla et al., Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies , JHEAp 34 (2022) 49 [arXiv:2203.06142].

[7] S. Weinberg, The Cosmological Constant Problem, Rev. Mod. Phys. 61 (1989) 1.

[8] Peebles, B. Ratra, The Cosmological Constant and Dark Energy, Rev. Mod. Phys. 75 (2003) 559 [astro-ph/0207347].

[9] T. Padmanabhan Cosmological constant: The Weight of the vacuum, Phys.Rept. 380 (2003) 235 [hep-th/0212290].

[10] J. Solà Peracaula, The Cosmological Constant Problem and Running Vacuum in the Expanding Universe, Phil. Trans. Roy. Soc. Lond. A, 380 (2022) 20210182 [arXiv:2203.13757].

[11] J.  Solà,  Cosmological Constant and Vacuum Energy:  Old and New Ideas’,    J.  Phys.  Conf. Ser., 453, (2013) 012015, [arXiv:1306.1527]; Vacuum Energy and Cosmological Evolution, AIP Conf.Proc. 1606 (2015) 1, 19 [arXiv:1402.7049].

[12] C.  Moreno-Pulido  and  J.  Solà  Peracaula,   Running  vacuum  in  quantum  field  theory  in curved spacetime: renormalizing ρ_vac without m⁴ terms, Eur.Phys.J.C 80 (2020) 692 [arXiv:2005.03164]; Renormalizing the vacuum energy in cosmological spacetime: implications for the cosmological constant problem, Eur.Phys.J.C 82 (2022) 551 [arXiv: 2201.05827].

[13] N.E. Mavromatos and J. Solà Peracaula, Stringy-running-vacuum-model inflation:  from pri- mordial gravitational waves and stiff axion matter to dynamical dark energy , Eur.Phys.J.ST 230 (2021) 2077 [arXiv:2012.07971].

[14] J. Solà Peracaula, A. Gomez-Valent, J. de Cruz Pérez and C. Moreno-Pulido, Running vacuum in the Universe: phenomenological status in light of the latest observations, and its impact on the σ₈ and H₀ tensions, Universe 9 (2023) 6, 262 [arXiv:2304.11157]; Running vacuum against the H₀ and σ₈ tensions, EPL 134 (2021) 19001 [arXiv:2102.12758].

[15] C.   Moreno-Pulido   and   J.   Solà   Peracaula,   Equation  of  state  of  the  running  vacuum, Eur.Phys.J.C 82 (2022) 1137 [arXiv:2207.07111].